THE PROJECT

Please see the ADSYNX tab for a novel powerful adaptive method for high-frequency signal adaptation, which was a core result from ADOPD.

Background

Neurons show an impressive variety of dendritic structures as shown below. At these dendrites, most of the incoming signals converge and information is transmitted via synapses contacting dendritic branches.

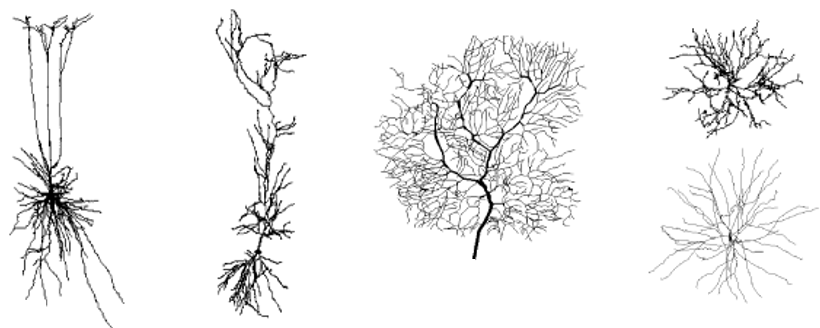
Recompiled from Gerstner et al. (2014)

Evidence exists that dendritic structures perform different types of computations (see figure below) for example (left) spatio-temporal filtering e.g. a low-pass operation, (middle) logical gating for information selection (here AND-gate operation) which relies of the coincidence of the incoming signals and (right) routing operations by letting signals pass using a “switch-like mechanism”. More such operations exist and – remarkably – all of them are subject to adaptation mechanisms based on changes of the synaptic transmission strength (“synaptic plasticity”).

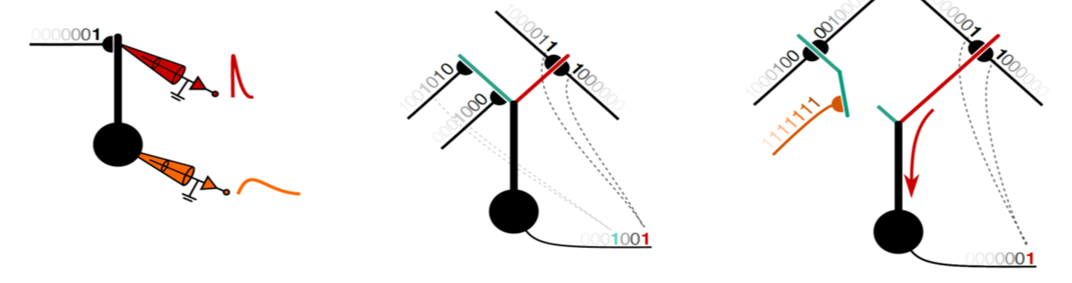
Recompiled from Payeur et al. (2019)

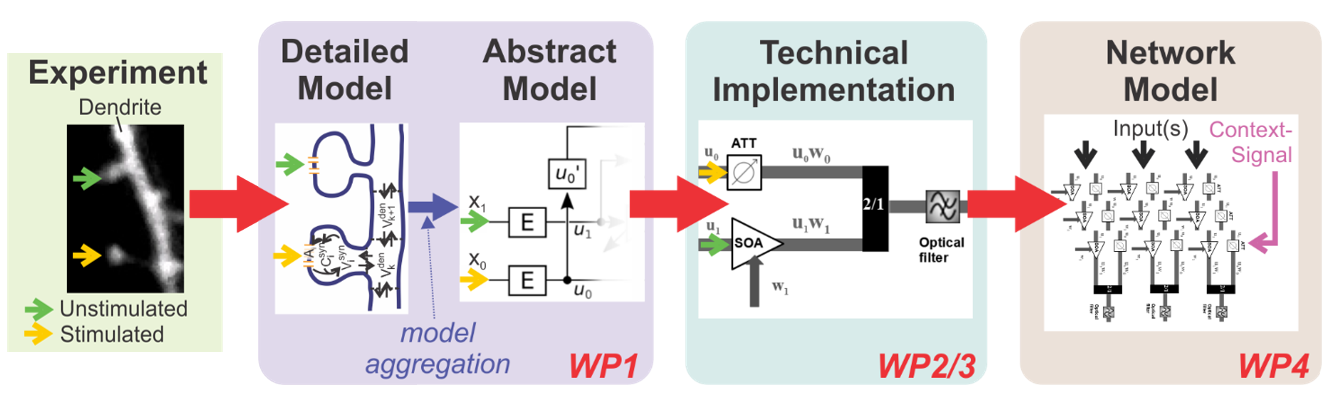
ADOPD addresses the question how neuronal dendrites perform adaptive (learnable) computations
and how this could be translated into optical (photonic) hardware.

Work Packages

The ADOPD project had four R&D work packages (see figure below).

WP1 is offering novel biophysical insights on heterosynaptic dendritic plasticity based on Calcium diffusion. The schematic below shows the diffusion setup.

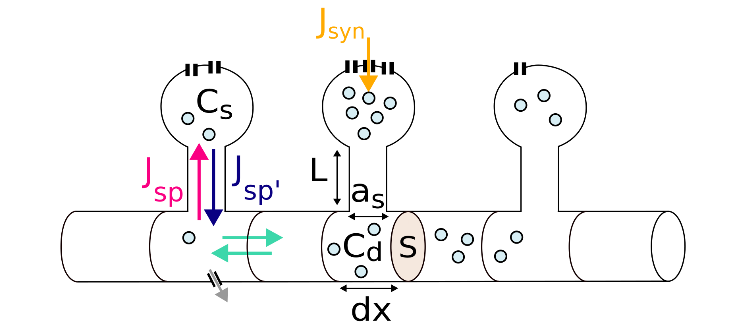
With this setup one can get different plasticity characteristics as shown next. Where this figure shows the synaptic weight change in response to single input spike at each spine. Here, the distance between spines is 1μm and we have 5 pairs of spikes. Various patterns are observed at different potentiation and depression thresholds.

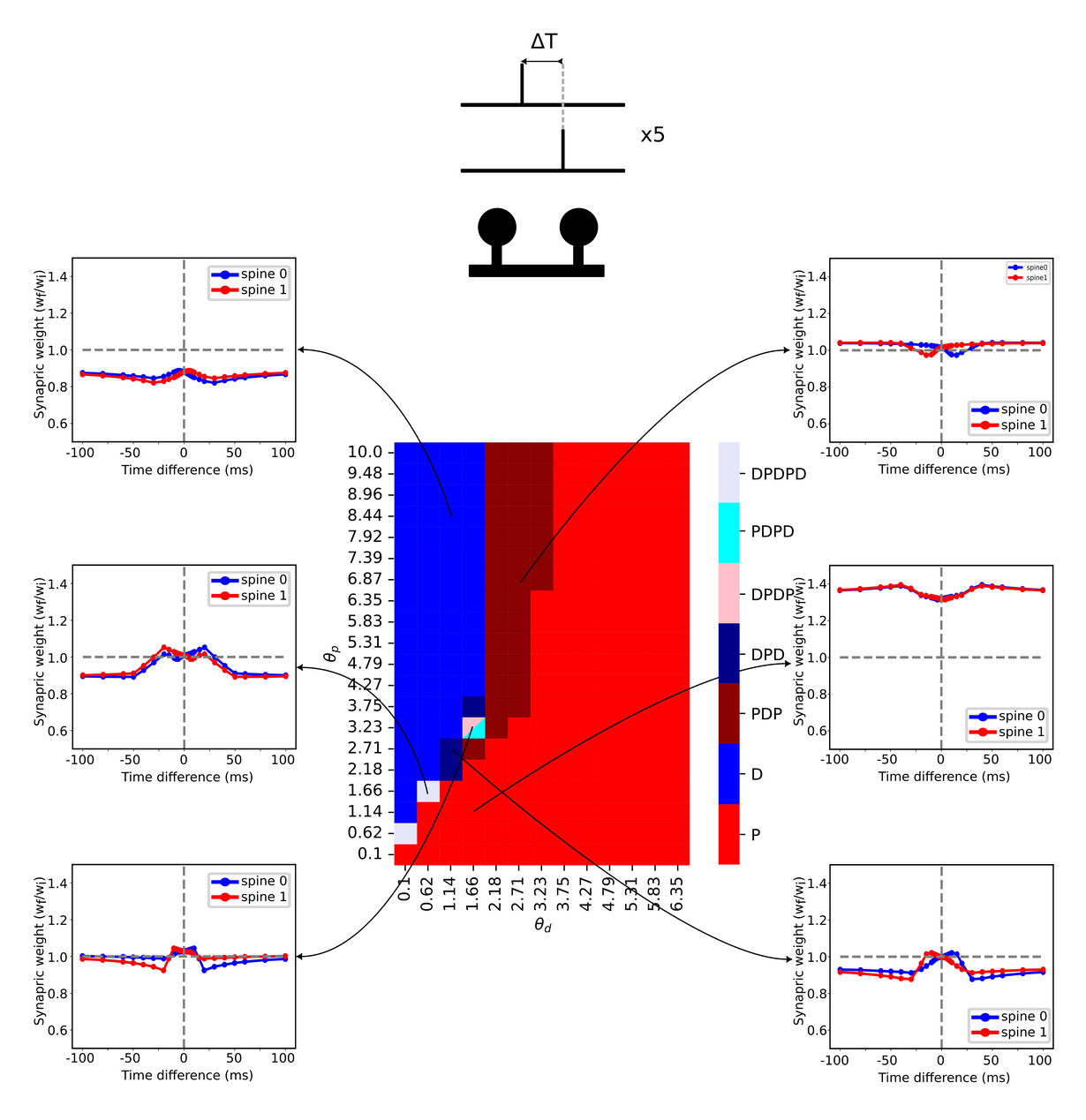
These investigations cannot directly be used for photonic implementation. Hence, part of the work in WP1 is dedicated to the translation of detailed biophysical theories into more abstract models suitable for transfer to hardware. Here we are focusing also on heterosynaptic plasticity by ways of the “Input Correlation (ICO)” learning rule (Porr & Wörgötter, 2006) shown below. In the ICO learning model the “reflex” behavior x₀ acts as a teacher signal training the synaptic weight w₁ in a heterosynaptic manner.

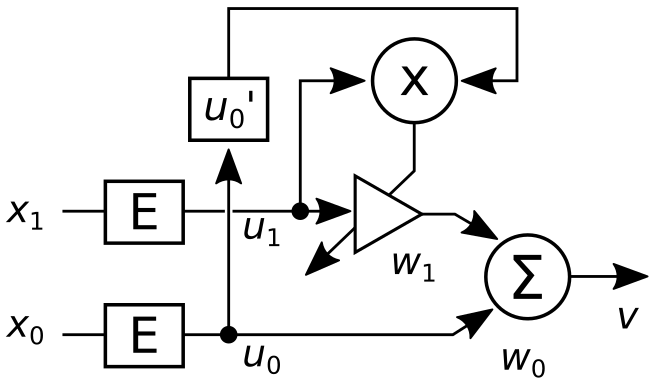
This rule has two convergence conditions. Learning will stop as soon as the reflex x₀ is eliminated or when both signals x₀ and x₁ occur at the same time, hence when they are synchronous. The latter condition has been used for the ADSYNX synchronization method.

The condition of x₀=0 has been used for photonics implementation of a closed-loop control problem in WP2.

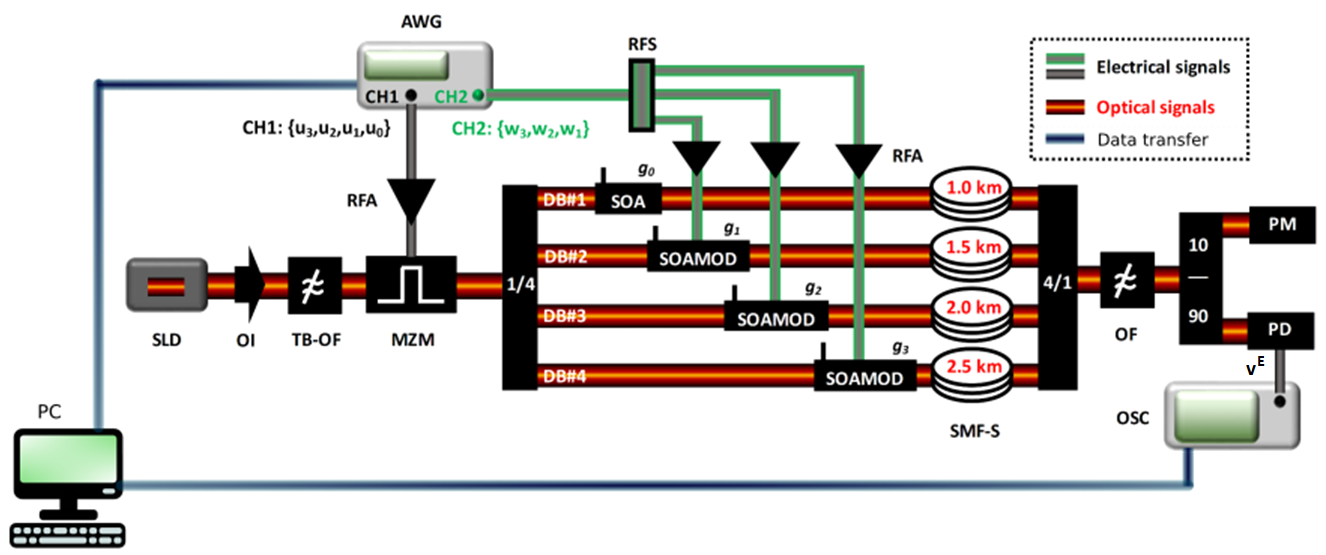
WP2 addresses the question how to implement the ICO rule using single mode fiber technology. The figure above depicts a photonic-circuity. The orange (gray, green) lines indicate optical (electrical) signals. The inputs u_i and the weights w_i are time-multiplexed in the arbitrary waveform generator (AWG) and physically demultiplexed in four different dendritic branches, by matching the time between different series u_i generated by the AWG with the length of the SMF-S fibers. The optical weights wi are calculated on a conventional computer (PC) from the output signal v_E, following the ICO rule, and applied from the AWG to the SOAMOD devices that perform the multiplication of u_i with the plastic weight w_i. The dendritic branch DB#1 is used as the reference for the ICO learning rule, thus it has a constant weight.

With this circuit it is possible to stabilize a system against disturbances. The circuit below, which has been built by the hardware of the figure above, performs the learning of a temperature stabilization task.

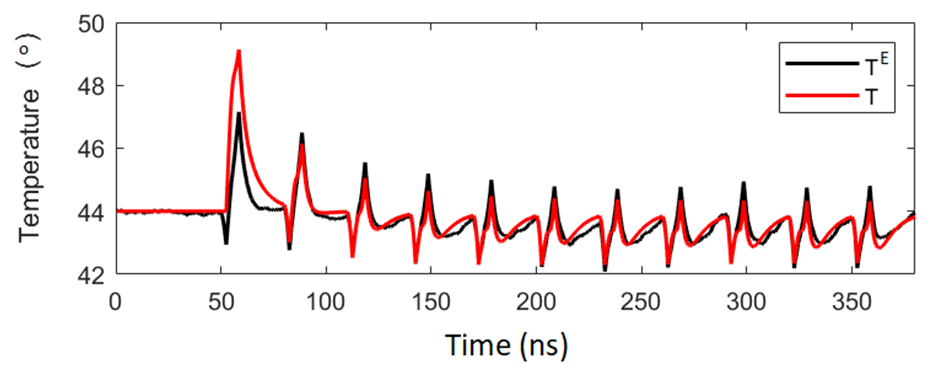
One can see (next figure) that after only 3 learning events temperature disturbance has been much reduced (red, in black there is the corresponding numerical simulation).

A hardware-based demonstrator has been created to demonstrate the closed loop operation of this circuit.

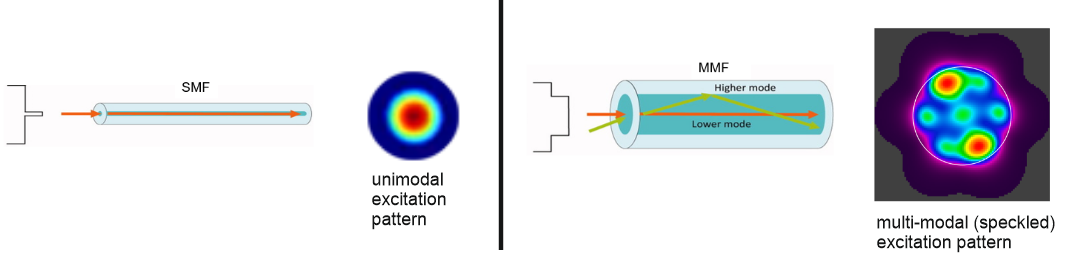
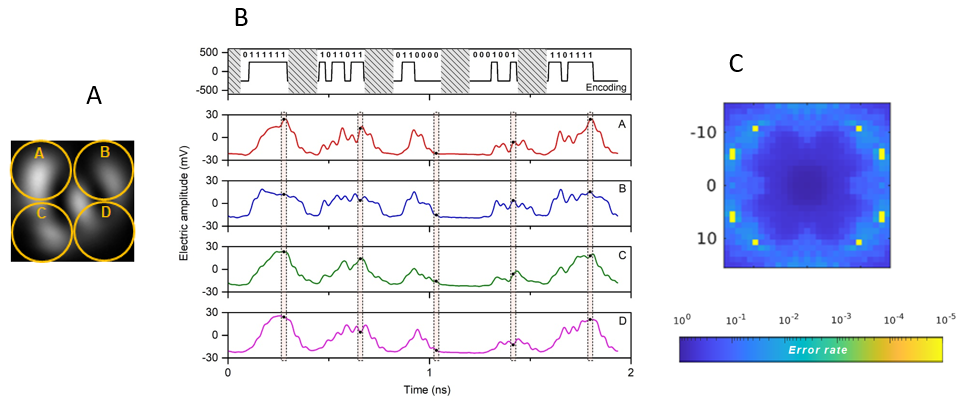
WP3 is performing significant ground work for abstracting dendritic functions into parallel optical computation via the use of different speckle patterns that arise in multi- or few-mode fibers (MMF, FMF, see figure above). This is an important conceptual step, as it may allow subsuming the computations of different dendritic branches, investigated in WPs 1 and 4, in a holographic manner into the same MMF or FMF. ADOPD focuses on FMFs, because of the lower complexity of the resulting speckle pattern and the resulting smaller sensitivity to noise in the read-out process. Accordingly, a new FMF, specific for our purpose, was fabricated. In the figure below, we used a 4-quadrant photo-diode detector array (A) and present different bit-patterns (light=1, dark=0) at the FMF (B, top). One can see that quadrants A-D are then differently strong activated (B, bottom). This allows for bit-pattern detection and the right panel below (C) plots the detection error against the entry axis of the input beam relative to the center of the fiber.

A hardware-based demonstrator has been created to demonstrate the bit-pattern recognition performance with FMFs.

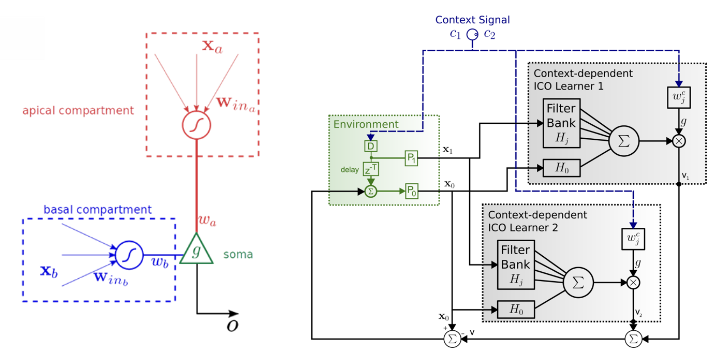
WP4 provides deeper insights into context-dependent dendritic processing on multiple branches using different structures and learning rules, especially also the ICO rule, which allows easy processing of context on different dendritic structures. The figure above suggests different roles for apical and basal dendrites, where the context signal is provided apically and the main signal is provided basally (left). To the right we show how it is possible to implement this in an adaptive manner using the ICO rule, which offers an avenue for photonic implementation of context dependent dendritic learning, too.

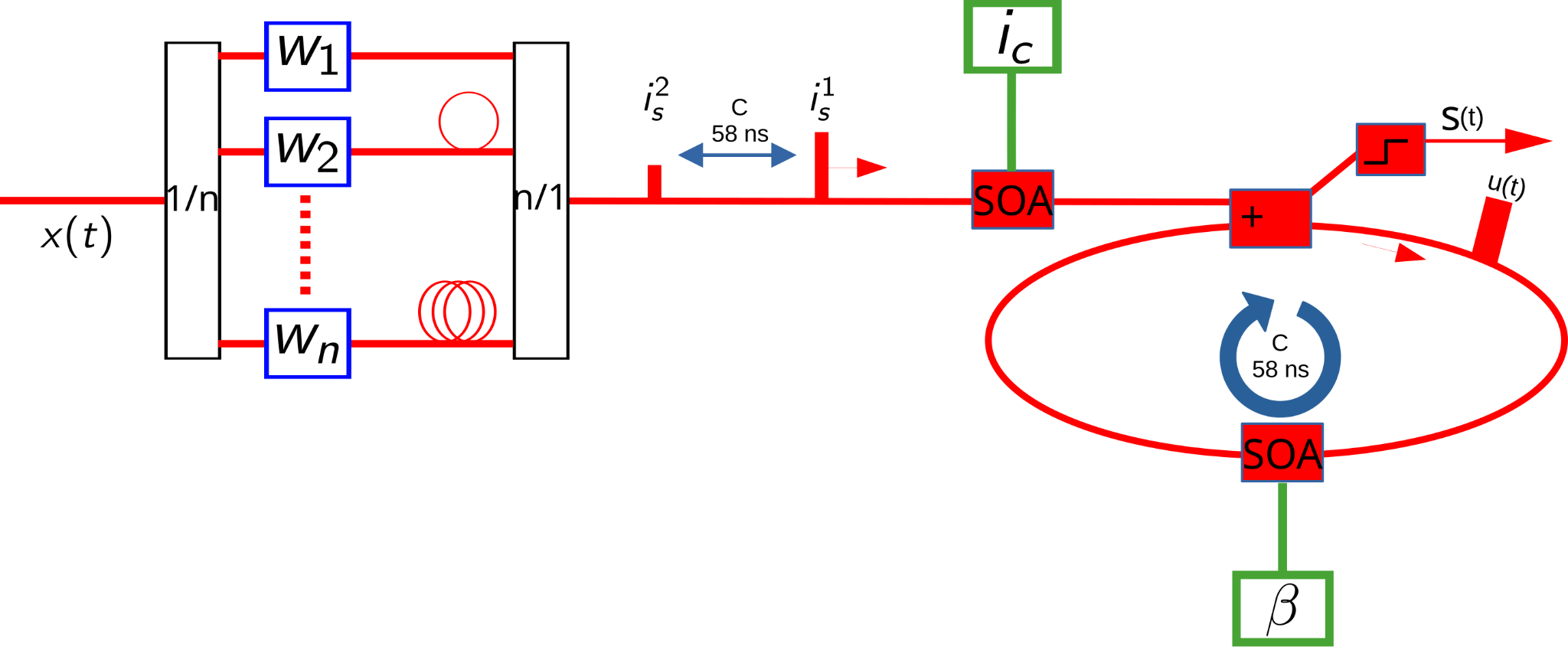
This can be implemented by photonic circuitry using the properties of an optical memory cell with a 58ns retention cycle (see Figure below). Show is here a schematic of the contextual Optical Memory Cell – context dependent Linear Integrate and Fire neuron (OMC-cLIF) model. The model combines an optical dendritic unit (ODU) with n synapses with an Optical Memory Cell (OMC). An SOA with learnable electrical current value is added between the ODU and the OMC. The current associated with a particular context is given by i_c and multiplicatively modulates the outgoing ODU light pulse i_s. The resulting interaction i_s × i_c is then added to the OMC state u(t).

With this circuit on reaches about 96% recognition accuracy for hand-gestures. A software-based demonstrator has been created to demonstrate this (Figure below).

Impact

The novel methods of ADOPD are already gradually creating impact on technology. Technology transfer and showcasing has been performed (see Outreach tab) and some aspects of ADOPD are now being pursued towards higher TRL levels (ADSYNX). The technology has also potential to reach out to society. This is due to the fact that neuromorphic computing technologies are powerful, because they reduce energy consumption while at the same time still supporting super-high-speed computation. This, combined with emulated neuronal plasticity at a spatially distributed structure (dendritic learning), is not only novel, but may gradually lead to systems where speed and low-power are paired with adaptation.

References